Chapter 1 - Introduction to Vectors
Three fundamental ideas
1.1 Vector addition and linear combinations
1.2 The dot product of two vectors and the length
1.3 Matrices , linear equations , solutions
The heart of linear algebra is in two operations - both with vectors. We add vectors to get . We multiply them by numbers and to get and . Combining those two operations gives the linear combination .
1.1 Vectors and Linear Combinations
We work with column vectors. A vector in 2D space has two components:
Column Vector
first component of second component of
We can perform two basic operations: vector addition and scalar multiplication.
Vector Addition & Subtraction
Add or subtract vectors component-wise:
Scalar Multiplication
Multiply each component by a scalar :
The number is called a scalar.
Zero Vector
The vector with all components equal to zero is the zero vector, denoted .
Note that . The zero vector is essential in any vector space.
Combining scalar multiplication and vector addition creates linear combinations.
Linear Combination
A linear combination of vectors and is given by:
where and are scalars.
Example Linear Combination
For and , the linear combination with is:
The vectors (where ) lie along a line through the origin and .
When is not on that line, the combinations fill the whole two-dimensional plane.
Starting from four vectors , , , and in four-dimensional space, their combinations are likely to fill the space - but not always. The vectors and their combinations could lie in a plane or on a line within the 4D space.
Vector Representation
We can think of and represent a vector in several ways:
- As a column vector:
- As a row vector (transpose):
- As an arrow in the plane: from the origin to the point .
- As a point in the plane: .
Vectors in Three Dimensions
A Note on Notation
From now on is also written as .
The reason for the row form (in parentheses) is to save space. But is not a row vector!
The plane is replaced by three-dimensional space. Here are typical vectors:
The vector corresponds to an arrow in 3-space. Usually the arrow starts at the "origin" where the axes meet and the coordinates are . The arrow ends at the point with coordinates . There is a perfect match between the column vector and the arrow from the origin and the point where the arrow ends.
In three dimensions, is still found a component at a time. The sum has components , , and .
A typical linear combination of three vectors in three dimensions
Picture of vectors in multidimensional space
- The combinations fill a line through the origin .
- The combinations fill a plane through the origin .
- The combinations fill the three-dimensional space.
Review of The Key Ideas
- A vector in 2D space has two components: and .
- and .
- A linear combination of three vectors , , and is .
- Take all linear combinations of or and or , , . In three dimensions, those combinations typically fill a line, then a plane, then the whole space .
Worked Examples
Example 1.1 A:
Example 1.1 A
The linear combinations of and fill a plane in . Describe that plane. Find a vector that is not a combination of and - not on the plane.
Solution: The plane of and contains all combinations . The vectors in that plane allow any and .
Four vectors in that plane are and and and . The second component is always the sum of the first and thir components. Like most vectors, is not in the plane, because .
TODO: How to calculate it numerically?
Another description of this plane through is to know that is perpendicular to the plane. Section 1.2. will confirm that angle by testing dot products: and .
IMPORTANT
Perpendicular vectors have a dot product of zero.
Example 1.1 B:
Example 1.1 B
For and , describe all points with whole numbers and nonnegative numbers . Then add all vectors and describe all points .
Solution:
(1) The vectors are for whole numbers . They are equally spaced points along the -axis (the direction of ). They include , , , , .
(2) The vectors with fill a half-line. It is the positive -axis. This half-line starts at where . It includes and but not .
(1') Adding all vectors puts a vertical line through those equally spaced points. We have infinitely many parallel lines from (whole number , any number ).
(2') Adding all vectors puts a vertical line through the half-line of . We have infinitely many parallel lines from (nonnegative , any number ). The half-line starts at and goes to infinity in the direction of .
Example 1.1 C:
Example 1.1 C
Find two equations for and so that the linear combination of equals a given vector .
Solution: In applying mathematics, many problems have two parts:
- Modeling part: Express the problem by a set of equations.
- Computational part: Solve those equations by a fast and accurate algorithm.
Our example fits into a fundamental model for linear algebra:
For we will find formula for the 's. The elimination method in Chapter 2 succeeds far beyond . For greater than 1 billion, see Chapter 11.
Vector equation
is a vector equation.
Two ordinary equations are:
Each equation produces a line. The two lines cross at the solution and .
Matrix equation
The vector equation can be written as a matrix equation:
Problem Set 1.1 (TODO)
Vector Independence
For vectors to be in the same plane, they must be able to be expressed as linear combinations of at most 2 linearly independent vectors. Vectors that are linearly independent cannot all be in the same plane if there are more than two of them.
Linear Independence
Two linearly independent vectors define a plane. Three linearly independent vectors in 3D space define a 3D space, not a plane.
TODO: Question
How to check for linear independence?
Problems 1-9 are about addition of vectors and linear combinations
1. Describe geometrically (line, plane or all or ) all linear combinations of
a) thus they are linearly dependent and lie on the same line. They do not fill the plane.
b) Vector adds information about component, vector adds information about and components. Their linear combinations will fill a plane in .
c)
So the math does not add up. So whenever we have a linear combination we can see that all the elements are transformed in the same way. So in this case it would be linearly independent if all three elements in were . But the is not equal to the sum of the other two components (). It means they are not linearly dependent so we end up with three vectors that are all linearly independent so they add 3 dimensions of space so it fills all of the .
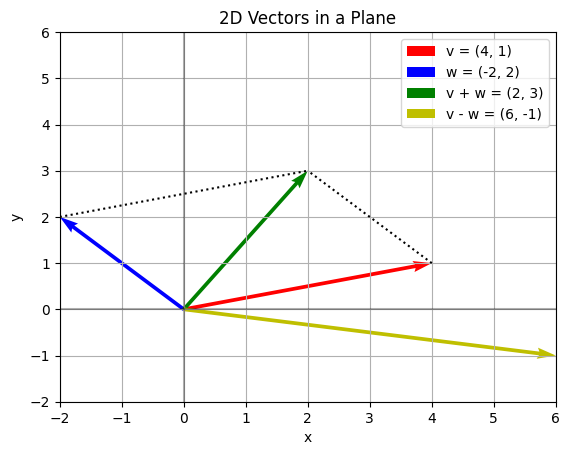
3. If and , compute and draw the vectors and .
So we get a set of four equations:
We can solve these equations in pairs.
Add the two equations:
Substituting into the first equation:
Now we can substitute and into the second pair of equations:
Add the two equations:
Substituting into the first equation:
So the vectors are:
4. From and , find the components of and .
so the components of are
For , we have:
The first component is and the second component is .
These vectors are linearly independent because they are not multiples of each other.\
5. Compute and . How do you know lie in a plane?
Data:
Solution :
Solution :
The vectors , , and are linearly independent because they do not lie on the same line or plane.
TODO: Draw it to investigate the linear independence of , , and .
6. Every combination of and has components that add to zero. Find and so that . Why is impossible?
Data:
Solution:
To find the components of the vector are:
So it gives us three equations:
Substituting into the second equation:
Substituting and into the third equation:
So the solution is and .
The impossible vector is impossible because the sum of the components of and is zero.
So the sum of the components of any linear combination of and is zero.
7. In the xy plane mark all nine of these linear combinations: + with and .
8. The parallelogram in Figure 1.1 has diagonal . What is its other diagonal? What is the sum of the two diagonals? Draw that vector sum.
Notebook with solution and plot Data:
The sum of the two diagonals is:
9. If three corners of a parallelogram are (1,1), (4,2) and (1,3), what are all three of the possible fourth corners? Draw two of them.
Problems 10-14 are about special vectors on cubes and clocks
Problems 15-19 go further with linear combinations of and
1.2 Lengths and Dot Products
Fundamental Ideas
1.1 The dot product of and is .
1.2 and are perpendicular because .
1.3 The length squared of is . The length is .
1.4 Then has length . Check: .
1.5 The angle between and has
1.6 The angle between and has . That angle is .
1.7 All angles have . So all vectors have .
The dot product or inner product
The dot product of two vectors and is defined as:
The dot product is the same as .
Example 1: The vectors v = (4,2) and w = (-1, 2) have a zero dot product:
The dot product is zero
Perpendicular vectors
Perpendicular vectors
Two vectors and are perpendicular if their dot product is zero:
The angle between them is .
Example 2: The equation for the see-saw (balance weights)
Put a weight of at the point and a weight of at the point . The -axis will balance on the center point (like a see-saw).
The vector of weights is and the vector of distances is .
The weights balance because the dot product is .
The weights times the distances: and give the "moments".
Example 3: Economics and business
We have three goods to buy and sell. Their prices are , , and . The quantities are , , and . Selling units at the price brings in . The total income (quantities times prices ) is the dot product in three dimensions:
A zero dot product means that that "the books balance". Total sales equal total purchases if . Then is perpendicular to (in three-dimensional space).
DEFINITION: Length of a vector
When the vector is , the dot product with itself is
Instead of a angle between vectors, we have a angle.
The answer is not zero because is not perpendicular to itself.
The length of the vector is the square root of :
DEFINITION: Unit vector
A unit vector is a vector whose length = . is a unit vector in the direction of .
Vector has length . We divide vector by its length to get the unit vector . Then (unit vector).
Note: The unit vector represents a direction in the plane and is essential in various applications, including physics and engineering.
The length of a four-dimensional vector would be:
Thus the vector has length . This is the diagonal through a unit cube in four-dimensional space. That diagonal in dimensions has length .
Example 4: Unit vectors and angles
The standard unit vectors along the and axes are written as and . In the plane, the unit vector that makes an angle with the -axis is:
The length of is because .
When , the horizontal unit vector is .
When , the vertical unit vector is .
At any angle, the components and produce because . These vectors reach out to the unit circle. Thus and are the and coordinates of a point on the unit circle.
The Angle Between Two Vectors
We stated that perpendicular vectors have . The dot product is zero when the angle is .
Angles between vectors
The dot product is when the angle between and is . The sign of immediately tells whether we are below or above a right angle.
POSITIVE: The angle is between and .
NEGATIVE: The angle is between and .
ZERO: The angle is .
The dot product reveals the exact angle .
Unit vectors and at angle have .
What if and are not unit vectors? Divide by their lengths to get and Then the dot product of those unit vectors gives: .
Cosine of the angle
The cosine of the angle between two vectors and is:
The angle is between and .
The cosine of the angle is between and .
Schwarz Inequality
The Schwarz Inequality states that for any vectors and , the following holds:
Whatever the angle, this dot product never exceeds one.
This inequality is fundamental in linear algebra and has various applications in mathematics and physics.
Triangle Inequality
The triangle inequality states that for any vectors and , the following holds:
This inequality is a fundamental property of vector spaces and has applications in various fields, including geometry and optimization.
Example 5: Find cosine theta for v = (2, 1) and w = (1, 2) and check both inequalities.
Solution:
By the Schwarz Inequality, is less than .\
By the triangle inequality, is less than .